Introduction
Welcome to OpenZL, the "missing ZKP library."
OpenZL is an open-source library for development of secure, high-performance, zero-knowledge applications. OpenZL aims to bridge the gap between high-level languages that miss valuable opportunities for optimization and low-level libraries that require extensive cryptographic expertise. We believe that bridging this gap can improve both the speed and security of ZK app development.
OpenZL takes a three-tiered approach to the problem:
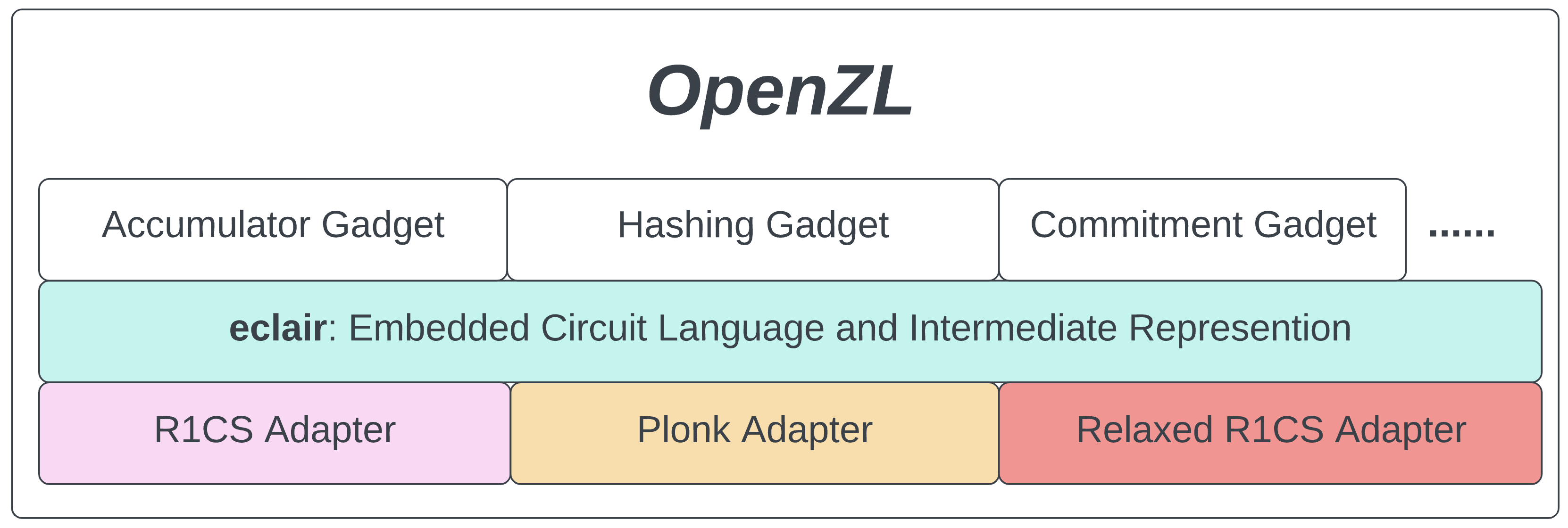
Gadget Layer
The high-level layer provides cryptographic "gadgets" such as accumulators, hash functions, commitment schemes, etc. These ready-to-go gadgets are intended for drop-in use in ZK applications. They are composable, allowing complex logic to be built from cryptographic primitives. The gadget library serves developers who want to access ZK without getting in the weeds.
Plugin Layer
Importantly, OpenZL gadgets make no assumptions about the ZK proving system they target. Instead, developers choose an appropriate proof system plugin to use whatever proving system works best for their application. These plugins form the low-level layer of OpenZL; this is where nitty-gritty, proof-system-specific optimization occurs.
Middle Layer: ECLAIR
Between the gadget layer and the proof system layer sits ECLAIR: the Embedded Circuit Language And Intermediate Representation. ECLAIR is a proof-system-agnostic language for circuit descriptions. Gadgets written in ECLAIR can target any of the ZK proving systems provided by low-level plugins. OpenZL thus achieves modularity at both the high and low level.
We will have much more to say on ECLAIR in the following chapters. For now, let us just emphasize our goals. We believe that ZK app development should be:
-
Fast: both in the sense that developers should be able to quickly start using and composing gadgets and in the sense that those gadgets should be optimized for speed.
-
Flexible: as new ZK proving systems appear, developers should be able to quickly adopt the latest technology. We should also de-duplicate the effort required for projects to switch over.
-
Secure: you shouldn't have to be an expert cryptographer to build secure applications. We should instead pool our expertise and package it in the form of safe cryptographic libraries.
-
Open-source: "NO" to walled gardens! "YES" to collaboration! OpenZL is and will remain open-source.
Please read on to learn more. For now these docs focus on ECLAIR, but we will soon update them with more explanation of the gadget and plugin layers.
Native vs Non-Native Computation
ECLAIR aims to unify and simplify the development of ZK applications by providing a circuit language that can target a myriad of zero knowledge proof systems. In doing so ECLAIR treats each ZK proof system as its own computational environment. Much as Rust source code can be compiled to executables for Linux, MacOS, or Windows, a circuit written in ECLAIR can target implementations of Groth16, Plonk-like proving systems, or any other proving backend for which an appropriate plugin exists.
In this framework it is useful to distinguish between "native" and "non-native" computational environments. "Native computation" is the everyday sort of computation that simply concerns itself with executing instructions on computer hardware; it produces no ZKP to attest to the computation's correctness. This is what computers do natively.
In ECLAIR, native computation is treated on an equal footing with other computational environments that do produce ZKPs of a computation's correctness. These are collectively referred to as "non-native computation." A proving system such as Groth16 is a non-native computational environment which provides a proof of correctness for any computation that can be represented as an arithmetic circuit. Likewise there are a variety of "Plonk-like" proving systems that achieve the same goal of performing a computation and providing a succinct argument of its correctness.
Given the variety of non-native computational environments and the current rate of innovation in ZK proving systems, it is desirable to describe circuits in a proving system agnostic representation like ECLAIR. The main advantages of doing so are:
- Agility: A circuit described in ECLAIR can target any proving system via plugins. Thus a developer can quickly switch the proving system used in their ZK app according to their needs. When the next hot new ZK proving system is discovered, a new plugin allows existing ECLAIR circuits to target that proving system.
- Correctness: Computation described in ECLAIR is performed the same way in all computational environments, native or non-native. This gives developers confidence that computations performed within a ZK proving system match their native version.
The COM Abstraction
As explained above, a computation described in ECLAIR can be carried out in various native or non-native computational environments. The computational environment is specified by choosing a type COM, short for "compiler."
We think of COM as a compiler that takes instructions written in ECLAIR and translates them to instructions for the target computational environment. In the case of native computation, COM would compile ECLAIR circuits to machine code for manipulating computer hardware. In the case of non-native computation, COM would compile ECLAIR circuits to a constraint representation such as R1CS for ZK proof generation.
For example, consider a trait Add that consists of a single function fn add for adding like types. Ordinarily, the signature of this function would be
#![allow(unused)] fn main() { fn add(lhs: Self, rhs: Self) -> Self }
But in ECLAIR, we include a generic type COM to define a trait Add<COM> for addition in an arbitrary computational environment. The signature of fn add becomes
#![allow(unused)] fn main() { fn add(lhs: Self, rhs: Self, compiler: &mut COM) -> Self }
In an ECLAIR circuit we may see a line like
#![allow(unused)] fn main() { output = add(lhs, rhs, &mut compiler); }
In the case of non-native computation, this results in a constraint being added to enforce output = lhs + rhs in whatever constraint system is appropriate to that computational environment. A circuit described using the Add<COM> trait can be compiled to any proving system that has a type implementing Add<COM>.
The Native Compiler Default COM = ()
In native computation there is no correctness proof and therefore no constraints for the compiler to generate. In this case ECLAIR hands off compilation to the Rust compiler to produce machine code. The native equivalent of an unsatisfied circuit is a computation that produces a runtime error. ECLAIR uses the unit type COM = () to represent the native compiler.
ECLAIR traits generally use the native compiler by default, such as Add<COM = ()>. This means that unless a ZK proving system is chosen by specifying some other type for COM, the computation will be carried out natively. When implementing ECLAIR traits for the native compiler, we still need to include the compiler argument in function signatures. For native-only computation this looks like
#![allow(unused)] fn main() { output = add(lhs, rhs, &mut ()); }
ECLAIR Standard Library
We explained in the previous section that ECLAIR achieves compatibility with various proof systems through its COM abstraction, which regards each ZK proving system as its own computational environment. ECLAIR makes minimal assumptions on the inner workings of each computational environment in an attempt to stay general enough to target a wide variety of ZK proving systems.
ECLAIR does, however, include a standard library of traits and types that will be relevant to nearly all COM types. We model this ECLAIR Standard Library on the Rust Standard Library. Whenever possible, ECLAIR uses the same API as Rust, with minimal changes to accommodate the COM abstraction.
Like the Rust standard library, ECLAIR's standard library is not strictly required; ECLAIR can handle compiler types that for whatever reason do not include implementations of the standard library traits. However, common compiler types will have implementations of most standard library traits, if not all of them.
We recommend reading through this chapter as a way to familiarize oneself with common patterns in ECLAIR. Most readers will be familiar with the Rust standard library and can ease their way into the COM abstraction by comparing ECLAIR's standard library traits to their counterparts in the Rust standard library. (The Bool and Num sections are not so Rust-like, but the Cmp and Ops sections are.)
Bool
Any reasonable computational environment has a notion of boolean type, but not all environments represent this concept in the same way. Native computation operates directly on bits and therefore has a natural notion of boolean type: a single bit. However a non-native environment such as a ZK proving system may lack a natural boolean type. In order for ECLAIR to express bit-wise operations or truth-valued comparisons in these environments, we need to specify how each COM type executes boolean operations.
Has<bool>
First we must specify a given compiler's boolean type. We do so through the eclair::Has trait:
#![allow(unused)] fn main() { /// Compiler Type Introspection pub trait Has<T> { /// Compiler Type /// /// This type represents the allocation of `T` into `Self` as a compiler. /// Whenever we need to define abstractions that require the compiler to /// have access to some type internally, we can use this `trait` as a /// requirement of that abstraction. type Type; } }
The Has<T> trait is implemented for a compiler type COM to specify how the type T is represented within COM's computational environment. The native compiler COM = () always represents T as T, so it implements Has<T> for any type T.
To see the usefulness of Has<T>, suppose COM corresponds to a ZK proving system such as Groth16 that represents computation as a R1CS over some finite field F. We can call this compiler type R1CS<F>.
In this setting there are no "bits," only finite field elements. Thus we need to choose how to represent bits. A reasonable choice would be to use the field F itself, perhaps with the convention that the zero element represents the boolean 0 and any non-zero element represents the boolean 1. We would specify this choice by an implementation:
#![allow(unused)] fn main() { impl Has<bool> for R1CS<F> { type Type = FVar; } }
Here FVar is a type that represents variables in the R1CS that can have values in F. With this implementation we specify that the R1CS<F> compiler represents booleans as variables with values in F.
Has<bool> is a necessary trait for a compiler type to make sense of many natural operations such as comparison, conditional switching, assertion, etc. For example, an == comparison between two variables in COM produces a boolean truth value; this truth value must itself be represented somehow within COM, hence the requirement COM: Has<bool> in order for equality comparisons to be possible in COM. See Cmp for more on comparisons in ECLAIR.
Assert
An example of an ECLAIR trait that requires Has<bool> is Assert:
#![allow(unused)] fn main() { /// Assertion pub trait Assert: Has<bool> { /// Asserts that `bit` reduces to `true`. fn assert(&mut self, bit: &Bool<Self>); /// Asserts that all the items in the `iter` reduce to `true`. #[inline] fn assert_all<'b, I>(&mut self, iter: I) where Self: Assert, Bool<Self>: 'b, I: IntoIterator<Item = &'b Bool<Self>>, { iter.into_iter().for_each(move |b| self.assert(b)); } } }
If compiler is of a type COM that implements Assert then compiler.assert(bit) should generate a constraint that is satisfied if and only if bit represents true according to COM's implementation of Has<bool>. In the native compiler COM = () the computation produces a runtime error if bit = false.
The requirement COM: Assert is a prerequisite for the trait PartialEq<Rhs, COM>. More on that in Cmp.
Conditional Selection and Swap
Another common operation involving booleans is selection, expressed in ECLAIR through the ConditionalSelect<COM> trait:
#![allow(unused)] fn main() { /// Conditional Selection pub trait ConditionalSelect<COM = ()> where COM: Has<bool>, { /// Selects `true_value` when `bit == true` and `false_value` when `bit == false`. fn select( bit: &Bool<COM>, true_value: &Self, false_value: &Self, compiler: &mut COM ) -> Self; } }
If an ECLAIR circuit contains the line
#![allow(unused)] fn main() { output = select(bit, true_value, false_value, &mut compiler); }
then this generates a constraint in compiler that enforces output == true_value if bit represents true and output == false_value otherwise. Of course this only makes sense if compiler knows how to interpret bit as a boolean value, hence the requirement COM: Has<bool>.
A similar operation is conditionally swapping values based on a boolean. For this we have the ConditionalSwap<COM> trait:
#![allow(unused)] fn main() { /// Conditional Swap pub trait ConditionalSwap<COM = ()> where COM: Has<bool>, { /// Swaps `lhs` and `rhs` whenever `bit == true` and keeps /// them in the same order when `bit == false`. fn swap( bit: &Bool<COM>, lhs: &Self, rhs: &Self, compiler: &mut COM ) -> (Self, Self); } }
This trait is self-explanatory.
Cmp
Comparison is expressed in Rust through the traits PartialEq and Eq. ECLAIR has analogues of these that explicitly mention the compiler COM to specify the computational environment where comparison occurs. As in Rust, Eq is simply a sub-trait of PartialEq used to indicate that a partial equivalence relation is actually a true equivalence relation.
The ECLAIR equivalent of PartialEq is
#![allow(unused)] fn main() { /// Partial Equivalence Relations pub trait PartialEq<Rhs, COM = ()> where COM: Has<bool>, { /// Returns `true` if `self` and `rhs` are equal. fn eq(&self, rhs: &Rhs, compiler: &mut COM) -> Bool<COM>; /// Returns `true` if `self` and `rhs` are not equal. fn ne(&self, other: &Rhs, compiler: &mut COM) -> Bool<COM> where Bool<COM>: Not<COM, Output = Bool<COM>>, { self.eq(other, compiler).not(compiler) } /// Asserts that `self` and `rhs` are equal. /// /// # Implementation Note /// /// This method is an optimization path for the case when /// comparing for equality and then asserting is more expensive /// than a custom assertion. fn assert_equal(&self, rhs: &Rhs, compiler: &mut COM) where COM: Assert, { let are_equal = self.eq(rhs, compiler); compiler.assert(&are_equal); } } }
As with most traits in the ECLAIR Standard Library, PartialEq differs from its pure Rust equivalent mainly by the addition of the COM type and an argument compiler: &mut COM in the function signatures. This allows ECLAIR to generate appropriate constraints whenever COM specifies a ZK proving system.
For example, when an ECLAIR circuit contains the line
#![allow(unused)] fn main() { output = lhs.eq(rhs, &mut compiler); }
this means that compiler will allocate a variable output of COM's boolean type and constraint output to carry the truth value of lhs == rhs.
Besides the compiler argument, the main difference from Rust's PartialEq trait is the added method fn assert_equal. The reason for including this method is that in some ZK proving systems it may be possible to assert equality using fewer constraints than separate calls to PartialEq::eq and Assert::assert. In such situations, the implementation of PartialEq<COM> should replace the blanket implementation here with the more optimized version. This is an example of the sort low-level, COM-specific optimizations that ECLAIR allows.
Num
This module provides some useful traits and types for numerical operations. Currently it provides the traits Zero, One, and AssertWithinBitRange as well as an UnsignedInteger type for ECLAIR.
Zero, One
These traits can be implemented for a type T relative to a compiler COM in order to indicate that COM understands a notion of zero/one value for T. Moreover, the trait specifies how COM determines whether a given instance of T is equal to that zero/one value:
#![allow(unused)] fn main() { /// Additive Identity pub trait Zero<COM = ()> { /// Verification Type type Verification; /// Returns the additive identity for `Self`. fn zero(compiler: &mut COM) -> Self; /// Returns a truthy value if `self` is equal to the additive identity. fn is_zero(&self, compiler: &mut COM) -> Self::Verification; } }
Note the Verification type, which allows fn is_zero to output "truthy values" in whatever sense is appropriate for COM. For the native compiler COM = () we would choose Verification = bool. For a compiler such that COM: Has<bool>, we would likely choose Verification = Bool<COM> to be this compiler's boolean type. (Note, however, that we do not require that COM: Has<bool> for this trait.)
The trait One is similar to Zero:
#![allow(unused)] fn main() { /// Multiplicative Identity pub trait One<COM = ()> { /// Verification Type type Verification; /// Returns the multiplicative identity for `Self`. fn one(compiler: &mut COM) -> Self; /// Returns a truthy value if `self` is equal to the multiplicative identity. fn is_one(&self, compiler: &mut COM) -> Self::Verification; } }
Bit Range Assertion
Range checks arise frequently in ZK circuits. One reason is that the primitive data type in a ZK proving system is often a finite field element. When we use one of these finite field elements to represent a quantity such as a 20-byte ETH address we need to ensure that the field element really is within the correct range.
In the native computation setting this is a straightforward comparison between the finite field element (represented as a positive integer) and the maximum size of a 20-byte integer. However a non-native compiler needs to generate constraints that are satisfied only if the finite field element lies in the correct range.
ECLAIR's interface for range checks is the trait AssertWithinBitRange:
#![allow(unused)] fn main() { /// Within-Bit-Range Assertion /// /// # Restrictions /// /// This `trait` assumes that `BITS > 0` and does not currently support `BITS = 0`. /// In this case we would have an assertion that `x < 2^0 = 1` which is just that /// `x = 0` in most systems. For this usecase, the [`Zero`] `trait` should be /// considered instead. pub trait AssertWithinBitRange<T, const BITS: usize> { /// Asserts that `value` is smaller than `2^BITS`. fn assert_within_range(&mut self, value: &T); } }
This trait is implemented by a compiler type COM to specify how COM constrains values of type T to lie in the range specified by BITS. The line
#![allow(unused)] fn main() { compiler.assert_within_range::<BITS>(value); }
causes the compiler to generate constraints that are satisfied only if value lies within the range specified by BITS.
Unsigned Integers
The AssertWithinBitRange trait allows ECLAIR to handle unsigned integers within proof systems as finite field elements with a checked size. We define unsigned integers as a thin wrapper around a type T:
#![allow(unused)] fn main() { /// Unsigned Integer pub struct UnsignedInteger<T, const BITS: usize>(T); }
One should think of this construction as analogous to representing a boolean value with a u8. The u8 type is acting as a container for the boolean value. But this container is "too large" in the sense that many u8 values do not correspond to a boolean value. Before interpreting a u8 as a boolean it is necessary to check that its value lies in the range [0,1].
Similarly, when we work within a proving system over a finite field, we may need to use field elements as a container for unsigned integer types. In this case a range check is required to make sure that the value in this container really does have an interpretation as an unsigned integer of the given size.
The compiler type COM does not appear as part of the UnsignedInteger type, but it must be mentioned whenever we construct or mutate an UnsignedInteger:
#![allow(unused)] fn main() { impl<T, const BITS: usize> UnsignedInteger<T, BITS> { /// Builds a new [`UnsignedInteger`] over `value` asserting that it does not /// exceed `BITS`-many bits. pub fn new<COM>(value: T, compiler: &mut COM) -> Self where COM: AssertWithinBitRange<T, BITS>, { compiler.assert_within_range(&value); Self::new_unchecked(value) } /// Mutates the underlying value of `self` with `f`, asserting that after /// mutation the value is still within the `BITS` range. pub fn mutate<F, U, COM>(&mut self, f: F, compiler: &mut COM) -> U where COM: AssertWithinBitRange<T, BITS>, F: FnOnce(&mut T, &mut COM) -> U, { let output = f(&mut self.0, compiler); compiler.assert_within_range(&self.0); output } } }
Observe that both functions require the trait bound COM: AssertWithinBitRange<T, BITS>, meaning that the compiler must know how to constrain values of type T to the range specified by BITS. Before constructing an UnsignedInteger with fn new, compiler generates constraints that guarantee that T lies in the range specified by BITS. Similarly, fn mutate transforms an UnsignedInteger's value in some way and generates constraints to ensure that the result of the transformation still lies within range before returning a value.
When COM = () is the native compiler, fn new and fn mutate would panic if the inner value of type T exceeds the bit-range. In non-native computation, compiler would generate constraints that the inner value does not satisfy, resulting in an unsatisfied constraint system.
These functions can be seen at work in the implementation of Add and AddAssign for UnsignedInteger:
#![allow(unused)] fn main() { impl<T, COM, const BITS: usize> Add<Self, COM> for UnsignedInteger<T, BITS> where T: Add<T, COM>, COM: AssertWithinBitRange<T::Output, BITS>, { type Output = UnsignedInteger<T::Output, BITS>; fn add(self, rhs: Self, compiler: &mut COM) -> Self::Output { Self::Output::new(self.0.add(rhs.0, compiler), compiler) } } impl<T, COM, const BITS: usize> AddAssign<Self, COM> for UnsignedInteger<T, BITS> where COM: AssertWithinBitRange<T, BITS>, T: AddAssign<T, COM>, { fn add_assign(&mut self, rhs: Self, compiler: &mut COM) { self.mutate(|lhs, compiler| lhs.add_assign(rhs.0, compiler), compiler); } } }
As a thin wrapper around T, UnsignedInteger<T, BITS> inherits many implementations from T. But not all operations that can be performed on T result in a valid UnsignedInteger. For example, fn add uses the UnsignedInteger::new function to construct its return value, telling compiler to constrain that return value to the bit-range. Similarly fn add_assign calls fn mutate to mutate the value, again generating constraints that enforce a range check on the mutated value.
Checked vs Unchecked
Looking at the body of the UnsignedInteger::new method we see that after a range check it uses fn new_unchecked to construct its return value. ECLAIR exposes fn new_unchecked as a public function because it allows for optimizations in instances where range checks are unnecessary.
For example, if T implements Zero<COM> or One<COM> then we know that T's zero/one value will pass any range check (we require BITS >= 1 for range checks, see AssertWithinBitRange above). Thus the implementation is:
#![allow(unused)] fn main() { impl<T, const BITS: usize, COM> Zero<COM> for UnsignedInteger<T, BITS> where T: Zero<COM>, { type Verification = T::Verification; fn zero(compiler: &mut COM) -> Self { Self::new_unchecked(T::zero(compiler)) } fn is_zero(&self, compiler: &mut COM) -> Self::Verification { self.0.is_zero(compiler) } } }
In this instance it would be wasteful to add a range check to the value T::zero(compiler) because the contract of the Zero trait guarantees that this is within range. The same holds for T::one(compiler) in the implementation of One<COM>.
Another example where the unchecked construction should be used is the ConditionalSelect<COM> trait (see Bool):
#![allow(unused)] fn main() { impl<T, const BITS: usize, COM> ConditionalSelect<COM> for UnsignedInteger<T, BITS> where COM: Has<bool>, T: ConditionalSelect<COM>, { fn select(bit: &Bool<COM>, true_value: &Self, false_value: &Self, compiler: &mut COM) -> Self { Self::new_unchecked(T::select(bit, &true_value.0, &false_value.0, compiler)) } } }
Again it is appropriate to use unchecked construction because both true_value and false_value are of type UnsignedInteger and so it would be wasteful to perform another range check on their inner values.
Ops
ECLAIR has analogues of many of Rust's overloadable operators. These are the traits like Neg, Add, Mul, etc that overload the behavior of the -, +, * operators.
By now you can probably guess how ECLAIR defines analogues of these traits: function signatures pick up a mutable reference compiler: &mut COM to a compiler type and use this to generate constraints, when appropriate. For the native compiler COM = (), each trait is identical to its pure Rust analogue.
For example, the pure Rust trait Add<Rhs>:
#![allow(unused)] fn main() { pub trait Add<Rhs = Self> { type Output; fn add(self, rhs: Rhs) -> Self::Output; } }
is replaced with the ECLAIR trait Add<Rhs, COM>:
#![allow(unused)] fn main() { pub trait Add<Rhs = Self, COM = ()> { type Output; fn add(self, rhs: Rhs, compiler: &mut COM) -> Self::Output; } }
Now a line like
#![allow(unused)] fn main() { output = lhs.add(rhs, &mut compiler); }
causes compiler to allocate a variable output and constrain the value of output to be the sum lhs + rhs.
This straightforward transformation of traits is carried out for the following traits: Neg, Not, Add, BitAnd, BitOr, BitXor, Div, Mul, Rem, Shl, Shr, Sub, AddAssign, BitAndAssign, BitOrAssign, BitXorAssign, DivAssign, MulAssign, RemAssign, ShlAssign, ShrAssign, SubAssign. See the Rust documentation of these traits for more information.
Compiler Reflection
When some type T implements Add<COM>, this means that the compiler type COM knows how to generate constraints that enforce correct addition of values of type T. It can be useful to express this as a property of COM rather than a property of T, which ECLAIR does through "compiler reflection."
When T: Add<COM>, compiler reflection means that COM: HasAdd<T>. Explicitly, the HasAdd<T> trait is
#![allow(unused)] fn main() { pub trait HasAdd<L, R = L> { /// Output Type /// The resulting type after applying the `+` operator. type Output; /// Performs the `lhs + rhs` operation over the /// `self` compiler. fn add(&mut self, lhs: L, rhs: R) -> Self::Output; } }
So the line
#![allow(unused)] fn main() { output = lhs.add(rhs, &mut compiler); }
is equivalent to
#![allow(unused)] fn main() { output = compiler.add(lhs, rhs); }
For each of the traits listed above we include an implementation of the corresponding reflection trait:
#![allow(unused)] fn main() { impl<COM, L, R> HasAdd<L, R> for COM where L: Add<R, COM> { fn add(&mut self, lhs: L, rhs: R) -> Self::Output { lhs.add(rhs, self) } } }
With this HasAdd trait we can now use a trait bound COM: HasAdd<T> to express the requirement that certain other ECLAIR traits or circuits make sense only for compilers that can add values of type T.
Allocation
The alloc module defines ECLAIR's interface for allocating values in a compiler. We use the term "allocation" here to refer to the process of declaring a variable in a ZK proof system and (maybe) assigning it a value. Note that we are not referring to memory-related abstractions like heap allocation.
Variables in a ZK proof system can be private witnesses, public inputs, constants, or some mixture of these. For example, in a merkle tree membership proof we would have variables representing the values stored:
- in some leaf of the tree
- along the path from that leaf to the root
- in the root of the tree.
In the simplest case, all those values have the same type -- perhaps a finite field element. But in a ZKP, all those values should be private except the root, which would be public. So the description of this circuit must distinguish between public and private variables.
ECLAIR calls this distinction the "allocation mode." There are four allocation modes:
-
Constant: values that are proper to the circuit description and never change. These are public quantities known at compilation time.
-
Public: values that are public but may change in each instance of the circuit. For example, the root hash of a merkle tree. These values need to be exposed to the verifier in a ZKP.
-
Secret: values that are private. These values are known only to the prover in a ZKP and are never revealed.
-
Derived: values that are a composite of some public and secret values. For example, if the above merkle tree proof were considered as a single object then its allocation mode would be derived because it consists of both private and public values.
The constant allocation mode is substantially different from the other three in that constants are known at compilation time, whereas a variable's value will not be known until execution time when an instance of the circuit is constructed. For this reason, ECLAIR uses different interfaces for allocation of constants and variables.
Constants
The interface for allocating constants in ECLAIR is the Constanttrait:
#![allow(unused)] fn main() { pub trait Constant<COM = ()> { /// Underlying Type type Type; /// Allocates a new constant from `this` into the `compiler`. fn new_constant(this: &Self::Type, compiler: &mut COM) -> Self; } }
So a type T that implements Constant<COM> has some "underlying type" Type that it represents. Given values of that underlying type, we introduce them into our circuit description using fn new_constant, which takes the underlying value this, allocates it in the compiler, and returns COM's representation of the allocated value. We then use this output in our circuit description.
Note that ECLAIR assumes almost nothing about what it means to be a "constant"; it is up to the compiler COM to define how constants should be represented and manipulated. The one assumption ECLAIR does make is that constant values are known at compilation time, i.e. they are a fixed part of the circuit description.
Variables
All other quantities whose values are not known at compilation time are considered to be "variables." ECLAIR allocates these using the Variable trait:
#![allow(unused)] fn main() { pub trait Variable<M, COM = ()> { /// Underlying Type type Type; /// Allocates a new unknown value into the `compiler`. The terminology "unknown" /// refers to the fact that we need to allocate a slot for this variable during /// compilation time, but do not yet know its underlying value. fn new_unknown(compiler: &mut COM) -> Self; /// Allocates a new known value from `this` into the `compiler`. The terminology /// "known" refers to the fact that we have access to the underyling value during /// execution time where we are able to use its concrete value for execution. fn new_known(this: &Self::Type, compiler: &mut COM) -> Self; } }
As with constants, variables have an underlying Type that they represent within COM. This means that some type T implementing Variable<M, COM> is a Type-valued variable. The generic type M specifies the allocation Mode, which can be Public, Private, or Derived.
As with the Constant allocation mode, ECLAIR makes no assumptions about what it means to be Public, Private or Derived in a given COM context. ECLAIR assumes only that a variable's value is not yet known at compilation time.
Known vs Unknown Allocation
Unlike constants, there are two ways of allocating variables: as known and unknown. Allocation using fn new_known requires the variable's concrete value this. Allocation using fn new_unknown merely tells the compiler that when execution occurs, a value of this Type will go here.
Of course execution cannot actually occur until all variables have been provided a value. Allocating variables before their values are known using fn new_unknown allows us to perform certain useful operations from the circuit description before execution time, akin to performing algebraic manipulations on physical formulae before substituting in concrete values for the variables.
For example, some proving systems require pre-computed prover and verifier keys. When these are circuit-specific, they must be extracted from a circuit description. Since this occurs before execution time, we need a circuit description that accounts for all of the variables without assigning them a concrete value. Therefore a description of the circuit using fn new_unknown to allocate variables is appropriate for computing the prover and verifier keys. At execution time, when the circuit is used to generate proofs, it is appropriate to allocate the same variables using fn new_known.
This suggests an important principle of circuit-writing in ECLAIR: it is generally useful to separate variable allocation from variable manipulation. That is, one should identify the variables whose values are provided as inputs, either public or private, by the prover. Then, taking those as inputs, one writes a function to describe how they are manipulated according to the circuit logic.
Example: Merkle Tree Membership
To illustrate this we return to the merkle tree membership example we started with above. The relevant input values are:
- a leaf value:
leaf: L - the values of all sibling nodes on a path from that leaf to the root:
path: P - a root value:
root: R
The first two kinds of values are private, so we require that L: Variable<Secret, COM> and P: Variable<Secret, COM>. The root value is public, so we require R: Variable<Public, COM>. The function that describes a merkle tree membership check would look something like this:
#![allow(unused)] fn main() { fn membership_check<L, P, R, COM>(leaf: L, path: P, root: R, compiler: &mut COM) where L: Variable<Secret, COM>, P: Variable<Secret, COM>, R: Variable<Public, COM> { // hash `leaf` with its sibling // hash the result with the next sibling in `path` // ... // assert that final result equals `root` } }
The body of this function will perform computations on the input variables, allocating new intermediate variables in the process and generating constraints within compiler. Because we've specified that leaf and path allocate as Secret and root allocates as Public, the constraint generation will occur in whatever way is appropriate for dealing with public and private variables in the context of COM.
To extract a circuit description while leaving the variable values unknown, we might do something like this:
#![allow(unused)] fn main() { // Construct an instance of the compiler let mut compiler = CompilerType::new(); // Allocate variables with unknown values let leaf = Leaf::new_unknown(&mut compiler); let path = Path::new_unknown(&mut compiler); let root = Root::new_unknown(&mut compiler); // Generate membership check constraints membership_check(leaf, path, root, &mut compiler); }
Now compiler has allocated all the intermediate variables for a membership check and generated the necessary constraints among them. We could then extract proving and verifying keys from it, or any other information that can be extracted from the circuit description without concrete values. Note that we cannot compute a ZKP from compiler, since this would require concrete values for the variables.
In order to compute a ZKP in an instance where we have concrete values, we would do something like this:
#![allow(unused)] fn main() { // Construct an instance of the compiler let mut compiler = CompilerType::new(); // Allocate variables with known values let leaf = Leaf::new_known(leaf_value, &mut compiler); let path = Path::new_known(path_value, &mut compiler); let root = Root::new_known(root_value, &mut compiler); // Generate membership check constraints membership_check(leaf, path, root, &mut compiler); // Compute proof let proof = compiler.prove(); }
This time the compiler was able to compute a ZKP because the variables were allocated with known values.
As mentioned above, it was useful in this example to separate allocation and manipulation. All manipulation occurs within fn membership_check, which takes arguments that are assumed to be already allocated in the compiler. This ensured that the same manipulations would be performed on the symbolic and concrete forms of these variables.
(Of course many new variables are allocated as fn membership_check performs its computation, but their values are not provided directly by the prover. Perhaps it is more correct to say that one should separate variable input from variable manipulation.)
Tutorial: Poseidon Permutation
The Poseidon permutation, defined in GKRRS '19 operates on vectors of field elements. For a fixed width, the permutation transforms a vector of width-many field elements in repeated rounds. Each round consists of the following operations:
- Add Round Keys: Add a constant to each component of the vector.
- S-Box: Raise each component of the resulting vector to a power (in a full round), or raise just one component of the vector to a power (in a partial round).
- MDS Matrix: Multiply the resulting vector by a constant matrix.
This tutorial will walk through building the Poseidon permutation in ECLAIR. All OpenZL tutorials are accompanied by code examples, see here. Note that this code differs somewhat from our optimized Poseidon implementation.
trait Specification
The Poseidon permutation requires a choice of finite field. We will keep this example generic by using a Rust trait Specification to specify our assumptions on the field and defining the Poseidon permutation relative to any type that implements Specification.
#![allow(unused)] fn main() { /// Poseidon Specification /// /// This trait defines basic arithmetic operations we use to define the Poseidon permutation. pub trait Specification<COM = ()>: Constants { /// Field Type used for Permutation State type Field; /// Field Type used for Permutation Parameters type ParameterField; /// Returns the zero element of the field. fn zero(compiler: &mut COM) -> Self::Field; /// Adds two field elements together. fn add(lhs: &Self::Field, rhs: &Self::Field, compiler: &mut COM) -> Self::Field; /// Adds a field element `lhs` with a constant `rhs` fn add_const(lhs: &Self::Field, rhs: &Self::ParameterField, compiler: &mut COM) -> Self::Field; /// Multiplies two field elements together. fn mul(lhs: &Self::Field, rhs: &Self::Field, compiler: &mut COM) -> Self::Field; /// Multiplies a field element `lhs` with a constant `rhs` fn mul_const(lhs: &Self::Field, rhs: &Self::ParameterField, compiler: &mut COM) -> Self::Field; /// Adds the `rhs` field element to `lhs` field element, updating the value in `lhs` fn add_assign(lhs: &mut Self::Field, rhs: &Self::Field, compiler: &mut COM); /// Adds the `rhs` constant to `lhs` field element, updating the value in `lhs` fn add_const_assign(lhs: &mut Self::Field, rhs: &Self::ParameterField, compiler: &mut COM); /// Applies the S-BOX to `point`. fn apply_sbox(point: &mut Self::Field, compiler: &mut COM); /// Converts a constant parameter `point` for permutation state. fn from_parameter(point: Self::ParameterField) -> Self::Field; } }
The trait requires two types, Field and ParameterField. The permutation acts on vectors of elements of type Field. The constant parameters that define the permutation are of type ParameterField. At first it may seem strange to distinguish between these two types, since they coincide for native computation of the Poseidon permutation. But remember that one of the reasons to use ECLAIR is to specify computation in a language that applies to both native and non-native computation.
In practice we may need to compute Poseidon in-circuit as part of a ZK-proof. In this case the type Field would be some representation of private witnesses to the circuit, whereas ParameterField would be public input constants. These are quite different types indeed! Therefore it is appropriate to treat them as distinct for now and let the compiler deal with them in whatever way is appropriate for the mode of computation specified by the type COM.
Keeping in mind that the Field type may represent in-circuit variables, it is easy to see that we need two distinct notions of add (and mul). When adding two in-circuit variables we use
#![allow(unused)] fn main() { fn add(lhs: &Self::Field, rhs: &Self::Field, compiler: &mut COM) -> Self::Field; }
but when adding a constant to a variable it is appropriate to use
#![allow(unused)] fn main() { fn add_const(lhs: &Self::Field, rhs: &Self::ParameterField, compiler: &mut COM) -> Self::Field; }
Although these two methods coincide for the native compiler type COM = (), in general they are distinct. This illustrates an important principle of circuit writing in ECLAIR: We describe circuits in a general language that applies to all modes of computation; this ensures that different instances of computation (native/in-circuit) agree. Often it is useful to keep the more "exotic" case of in-circuit computation in mind.
Note that we specify the default compiler type to be COM = (), meaning that by default we use the native compiler.
trait Constants
You may notice that the previous trait Specification extends a trait Constants. Constants is a trait specifying three constant parameters that belong to the definition of a Poseidon permutation:
#![allow(unused)] fn main() { pub trait Constants { /// Width of the Permutation /// /// This number is the total number `t` of field elements in the state which is `F^t`. const WIDTH: usize; /// Number of Full Rounds /// /// The total number of full rounds in the Poseidon permutation, including the first set of full /// rounds and then the second set after the partial rounds. const FULL_ROUNDS: usize; /// Number of Partial Rounds const PARTIAL_ROUNDS: usize; /// Half Number of Full Rounds /// /// Poseidon Hash first has [`HALF_FULL_ROUNDS`]-many full rounds in the beginning, /// followed by [`PARTIAL_ROUNDS`]-many partial rounds in the middle, and finally /// [`HALF_FULL_ROUNDS`]-many full rounds at the end. /// /// [`HALF_FULL_ROUNDS`]: Self::HALF_FULL_ROUNDS /// [`PARTIAL_ROUNDS`]: Constants::PARTIAL_ROUNDS const HALF_FULL_ROUNDS: usize = Self::FULL_ROUNDS / 2; /// Total Number of Rounds const ROUNDS: usize = Self::FULL_ROUNDS + Self::PARTIAL_ROUNDS; /// Number of Entries in the MDS Matrix const MDS_MATRIX_SIZE: usize = Self::WIDTH * Self::WIDTH; /// Total Number of Additive Rounds Keys const ADDITIVE_ROUND_KEYS_COUNT: usize = Self::ROUNDS * Self::WIDTH; } }
Here WIDTH is the length of the vector of field elements that the permutation acts on via addition and matrix multiplication. FULL_ROUNDS and PARTIAL_ROUNDS specify the number of full and partial rounds of iteration that are performed on the state vector to achieve the desired security level. The remaining constants are computed in terms of the first three; they specify the number of "Additive Round Keys" and the size of the "MDS Matrix."
struct State
Given some type S that implements the above Specification trait we next define a state for the permutation to act on. This state is a vector of length WIDTH. We'll use a struct State to represent it:
#![allow(unused)] fn main() { /// The state vector that a Poseidon permutation acts on. pub struct State<S, COM = ()>(Box<[S::Field]>) where S: Specification<COM>; impl<S, COM> State<S, COM> where S: Specification<COM>, { /// Builds a new [`State`] from `state`. pub fn new(state: Box<[S::Field]>) -> Self { assert_eq!(state.len(), S::WIDTH); Self(state) } /// Returns a slice iterator over the state. pub fn iter(&self) -> slice::Iter<S::Field> { self.0.iter() } /// Returns a mutable slice iterator over the state. pub fn iter_mut(&mut self) -> slice::IterMut<S::Field> { self.0.iter_mut() } } }
Observe that although the compiler type COM plays no direct role in the definition of the State vector, it must be mentioned because it provides the context to understand the trait Specification<COM>. When COM specifies some ZK proof system to compute the permutation in, the elements of State will represent witness variables and the operations performed on State will generate constraints in whatever representation COM specifies. Again we have the default COM = (), meaning that when no compiler type is specified State consists of native field elements and the operations performed on it are computed natively.
For Rust-related reasons we choose not to specify the width as part of State's type. Observe however that the constructor fn new enforces that State must have the size specified by S via the Constants trait.
struct Permutation
The final ingredient is the parameters, a collection of constants that define a particular instance of the Poseidon permutation. In each round the permutation adds some constants, the additive_round_keys, to the State and multiplies the State by a constant matrix, the mds_matrix. These pre-computed constants are considered to be part of the definition of a Poseidon permutation. For information on generating secure constants, please refer to GKRRS '19.
Since these parameters define a specific instance of the Poseidon implementation, we call this struct Permutation. We define the Permutation to be generic over a type S that implements Specification:
#![allow(unused)] fn main() { /// The constant parameters defining a particular instance /// of the Poseidon permutation. pub struct Permutation<S, COM = ()> where S: Specification<COM>, { /// Additive Round Keys additive_round_keys: Box<[S::ParameterField]>, /// MDS Matrix mds_matrix: Box<[S::ParameterField]>, /// Type Parameter Marker __: PhantomData<COM>, } }
The additive_round_keys can be thought of as a list of constants from F::ParameterField, whereas the mds_matrix should be thought of as a matrix; this struct carries the flattening of that matrix. The sizes of these arrays are determined by the same WIDTH parameter that determines the length of State. Again, we enforce these size constraints with the constructor rather than the type system:
#![allow(unused)] fn main() { impl<S, COM> Permutation<S, COM> where S: Specification<COM>, { /// Builds a new [`Permutation`] from `additive_round_keys` and `mds_matrix`. /// /// # Panics /// /// This method panics if the input vectors are not the correct size for the specified /// [`Specification`]. pub fn new( additive_round_keys: Box<[S::ParameterField]>, mds_matrix: Box<[S::ParameterField]>, ) -> Self { assert_eq!( additive_round_keys.len(), S::ADDITIVE_ROUND_KEYS_COUNT, "Additive Rounds Keys are not the correct size." ); assert_eq!( mds_matrix.len(), S::MDS_MATRIX_SIZE, "MDS Matrix is not the correct size." ); Self { additive_round_keys, mds_matrix, __: PhantomData, } } } }
fn full_round, fn partial_round
A full round of permutation begins by adding the next WIDTH-many additive round keys to the State vector, then applying the "S-box" to each entry of the vector. Observe that the S-box operation is part of the Specification trait, fn apply_sbox. This operation on field elements is typically exponentiation to the power 3, 5, or -1.
A partial round of permutation also adds the next WIDTH-many additive round keys to the State vector, but then applies the S-box only to first element of this vector. The reason for mixing full and partial rounds is explained in GKRRS '19.
Both rounds finish by applying the MDS Matrix to the State vector. Let's add these methods to the Permutation:
#![allow(unused)] fn main() { impl<S, COM> Permutation<S, COM> where S: Specification<COM>, { /// Returns the additive keys for the given `round`. #[inline] pub fn additive_keys(&self, round: usize) -> &[S::ParameterField] { let start = round * S::WIDTH; &self.additive_round_keys[start..start + S::WIDTH] } /// Computes the MDS matrix multiplication against the `state`. pub fn mds_matrix_multiply(&self, state: &mut State<S, COM>, compiler: &mut COM) { let mut next = Vec::with_capacity(S::WIDTH); for i in 0..S::WIDTH { let linear_combination = state .iter() .enumerate() .map(|(j, elem)| S::mul_const(elem, &self.mds_matrix[S::WIDTH * i + j], compiler)) .collect::<Vec<_>>(); next.push( linear_combination .into_iter() .reduce(|acc, next| S::add(&acc, &next, compiler)) .unwrap(), ); } mem::swap(&mut next.into_boxed_slice(), &mut state.0); } /// Computes a full round at the given `round` index on the internal permutation `state`. pub fn full_round(&self, round: usize, state: &mut State<S, COM>, compiler: &mut COM) { let keys = self.additive_keys(round); for (i, elem) in state.iter_mut().enumerate() { S::add_const_assign(elem, &keys[i], compiler); S::apply_sbox(elem, compiler); } self.mds_matrix_multiply(state, compiler); } /// Computes a partial round at the given `round` index on the internal permutation `state`. pub fn partial_round(&self, round: usize, state: &mut State<S, COM>, compiler: &mut COM) { let keys = self.additive_keys(round); for (i, elem) in state.iter_mut().enumerate() { S::add_const_assign(elem, &keys[i], compiler); } S::apply_sbox(&mut state.0[0], compiler); self.mds_matrix_multiply(state, compiler); } } }
Note that fn full_round and fn partial_round take the round number as an input; this is so that they will take correct constants for the given round. Note that they also take the compiler as an input. As we explained above, this enables these functions to generate constraints within the ZK proof system specified by the type COM. For example, when adding round constants the add_const_assign method will add a constraint to compiler that enforces the addition of a public constant to the secret witness. Similarly, fn mds_matrix_multiply generates constraints within compiler to enforce that state was multiplied by the MDS Matrix.
Again, when no COM type is specified the default COM = () simply performs native computation without any constraint generation. The advantage of ECLAIR's COM abstraction is the certainty that add_const_assign or mds_matrix_multiply always conform to the same definition whether they are being used in native or non-native computation.
Putting it all Together: fn permute
Finally we combine the pieces to define the full permutation:
#![allow(unused)] fn main() { impl<S, COM> Permutation<S, COM> where S: Specification<COM>, { /// Computes the full permutation without the first round. fn permute(&self, state: &mut State<S, COM>, compiler: &mut COM) { for round in 0..S::HALF_FULL_ROUNDS { self.full_round(round, state, compiler); } for round in S::HALF_FULL_ROUNDS..(S::HALF_FULL_ROUNDS + S::PARTIAL_ROUNDS) { self.partial_round(round, state, compiler); } for round in (S::HALF_FULL_ROUNDS + S::PARTIAL_ROUNDS)..(S::FULL_ROUNDS + S::PARTIAL_ROUNDS) { self.full_round(round, state, compiler); } } } }
This function simply performs as many partial and full rounds as specified in the Constants trait.
Proof System Plugins
One of the goals of OpenZL is to provide great flexibility with respect to ZK proof systems. Developers should focus on the business logic of their application without committing to a particular ZK proof system. ECLAIR makes this possible.
ECLAIR code describes computation in general terms that make minimal assumptions about the environment where that code will be executed. This is ideal in the early stage of production when we need a circuit description that conforms to our spec. But at some point we do have to turn words into actions and use ECLAIR code to create ZKPs. This is where plugins come in.
A proof system plugin provides the low-level instructions for variable allocation and constraint generation in a specific ZK proof system. The plugin defines how ECLAIR code is compiled to constraints and, ultimately, used to generate ZKPs.
As a technical note, it is not quite correct to say that a plugin targets a specific ZK proof system, but rather a specific implementation of a ZK proof system. For example, there is no such thing as a "Groth16 plugin"; rather, there is a plugin for the Arkworks implementation Ark-Groth16.